In mental operation and in everyday speech we have recourse to constructions in which relationship terms are refined or composed to enable identification of one or more entities from the context of another. For example, relationships are strung together as in phrases like his father's cousin or my child's school's head teacher; they are narrowed in scope, as in the definition of sister as female sibling and they are combined or aggregated such as in the definition of parent as mother or father. In technical contexts, programmers using high level programming languages have use of formal equivalents of these as means of expression of program logic and mathematicians too have their notational equivalents. In this section we are going to describe the significance of these constructions to entity modelling and to present a way of visualising them in diagrams.

In some cases a single term exists that can be used in place of a composite relational construction; kinship terms provide a rich source of examples: grandfather substitutes for male grandparent, aunt for parent's sister and so on. Linguists would say in such cases that the single term and the composite phrase were translational equivalents.

Different languages vary with respect to the common relational constructions for which there are single term translational equivalents. For example, from the realm of temporal relationships rather those of kinship, in the Alamblak language of Papua New Guinea there is a word yuanane whose meaning is two days removed from the present which is to say its English translational equivalent is the day before yesterday or day after tomorrow. There is of course no single term in English which is translationally equivalent.

In regard to kinship terms, the English language is poorly endowed compared to many other languages and in English we need rely on explicit constructions such as elder brother, maternal uncle, wife's brother, cousin on mother's side to articulate relationships for which there are single word translational equivalents in other languages. For example, in the Sudanese kinship system also know as the descriptive system and into which category falls ancient Latin there is a specific term for all of the close family relationships. In Latin for example amitinus is father's sister's son, patruelis is father's brother's son, matruelis is mother's sister's son and, completing the male cousins, consobrinus is mother's brother's son.

In the definition of ‘maternal grandfather’ as ‘mother's father’ the definiendum is a relationship between invididuals:

whereas the definiens is a phrasing which joins two relationships end to end:

The definition presupposes types as shown in figure 50.

This construction by which a new relationship is defined from two others joined end to end is known simply as a join and the constructed relationship, the definiendum‘maternal grandfather’, is said to be a join of the other two — in this case the join of the ‘mother’ relationship with the ‘father’ relationship. In definitions like this we shall put together definiendum and definiens is a single diagram:

There is no limit to the numbers of relationships which can be joined together, for example:

Being as both the mother and father relationships are many-one relationships then they can be classified as mathematical functions; the relational join in this special case is precisely the mathematical operation of functional composition. In mathematical notation the functional composition, written f o g, of two functions f and g is defined by :

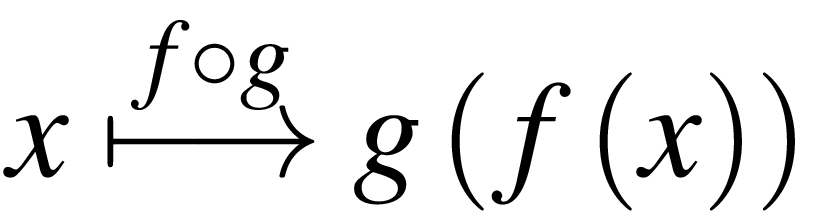
					maternalgrandfather = mother o father
				

					maternalgrandfather's mother = mother o father o mother
				

In computer software the / operation is often used in the definiens in these situations giving a construction which is sometimes described as a path or a navigation:

					mother/father/mother
				

The words navigate and navigation have come to be used in recent years in describing the activity of following links through the internet or through a web site and this usage has been entered into modern dictionaries. Pre-internet the words had widespread use among programmers describing the behaviour of programs moving along links between data entities. Immersed in the contexts of their programs, programmers will say I navigate here and I navigate their meaning that they program their programs to do this and this was echoed as earlier as 1960 by C.W.Bachman writing about the structural representations of data in that he called his paper "The programmer as navigator" . Family relationships again are a good source of examples. Suppose a program had to extract details of a person's maternal grandfather's mother. The programmer might say that they navigated:

This is of course to follow the join construction from left to right in the definiens of above.

A concept which has been used in theoretical contexts but not more widely is that of logical horizon (a term which can be found in Kant's 'Critique of Pure Reason'). Used in the entity modelling context, the logical horizon of an entity is the set of entities which can be reached from it by navigation of single valued relationships. Thus father, mother, their fathers and mothers and so on to all ancestors are said to be with in the logical horizon of a particular subject person entity.

Constructed relationships such as the joins that we have seen in () and () above encapsulate possible navigations. This gives us another way of expressing what the logical horizon of an entity is — we can define it to be the set of entities which can be reached by way of navigation of a single valued constructed relationship.

Whereas constructed relationships encapsulate directions for navigation from subject entities a set of directions such as:

In contrast to the definition of ‘maternal grandfather’, we can define the ‘parent’ relationship to be the aggregate of the ‘mother’ and ‘father’ relationships. The definiens is now ‘mother’and‘father’ instead of being ‘mother’then‘father’ In this case the two relationships, ‘father’ and ‘mother’ are put together side by side and the whole definition can be viewed like this:

‘A day two days removed from the present’, or yuanane¹, is also an aggregation since it is ‘day before yesterday’ aggregated with ‘day after tomorrow’ :

whereas ‘day before yesterday’ and ‘day after tomorrow’ are both joins:

‘Tomorrow’ and ‘yesterday’ are different ends of the one binary relationship of succession between days:

Joining ‘tomorrow’ with ‘tomorrow’ is equally joining ‘yesterday’ with ‘yesterday’. Consequently the yuanane relationship is it's own inverse, that is it is a symmetric relationship.

By expanding the definiens in the definition of yuanane and by also adding labels for all inverse relationships we get a single diagram:

If either of the relationships in a join is many-valued then the resulting relationship is many-valued. Thus maternal grandparent is many-valued because parent is:

The existence of translational equivalents poses a particular danger to entity modellers as we have discussed in the section on goodness of an entity model.