www.entitymodelling.org - entity modelling introduced from first principles - relational database design theory and practice - dependent type theory
Foundations of Data
Studies of the foundations of a subject should reveal something of its essential characteristics, its possibilities and its bounds; though study of the foundations of data modelling seems absent from the literature, such studies ought to reveal to us more directly than logic or philosophy something of the nature of our relationship to the world.
Indiscernibility of Identicals
What is data and what do we mean by data structure, by data model and by database? As so often it is easier to give examples in response to questions like these than to give real answers — flight lists, bank records, a star catalogue, a price list, a list of waypoints along a route, the runners in a race, the times of the tides — all these things can be presented as data typically containing names, both natural and coded, numerics as both ordinals and cardinals, measurements, dates and times, distances. Though we wouldn't usually put the matter so, asking What is data is like asking What is language? for data is a form of language, and asking How does data relate to the real world is a way of asking How does language relate to the real world?
Consider that in tabular presentations of data as well as in general discourse we often label things or more particularly number them arbitrarily. We make attributions of properties to individuals that in themselves do not have these properties; we do this of necessity when representing and communicating relationships between entities which are otherwise indiscernible from their properties. Thus, in a story of three, we can speak of the first, the second and the third, which is an arbitrary attribution, whereas in a story of an Englishman, a Scotsman and a Welshman we need for the telling no such arbitrary attribution. In the example tables used to present molecular structure in figure 7 each table of bonds makes double reference to entries in the atoms table by identifying entries by their ordinal position in the table; this is an arbitrary attribution of a number to each atom within the molecular structure. This arbitrary attribution is necessary because the entities within an individual molecular structure in and by themselves do not satisfy the logical principle of the identity of indiscernibles. In the study of Logic to accept this principle is to accept that no two distinct individuals/objects/things can be exactly the same in all of their properties. Logician Max Black suggested as a counter example to the principle a completely symmetric universe populated only by two distinct spheres; in such a universe the principle does not hold — the two spheres are indiscernible but not identical; to put it another way, there is no definite description that can be applied to one sphere that does not apply to the other.
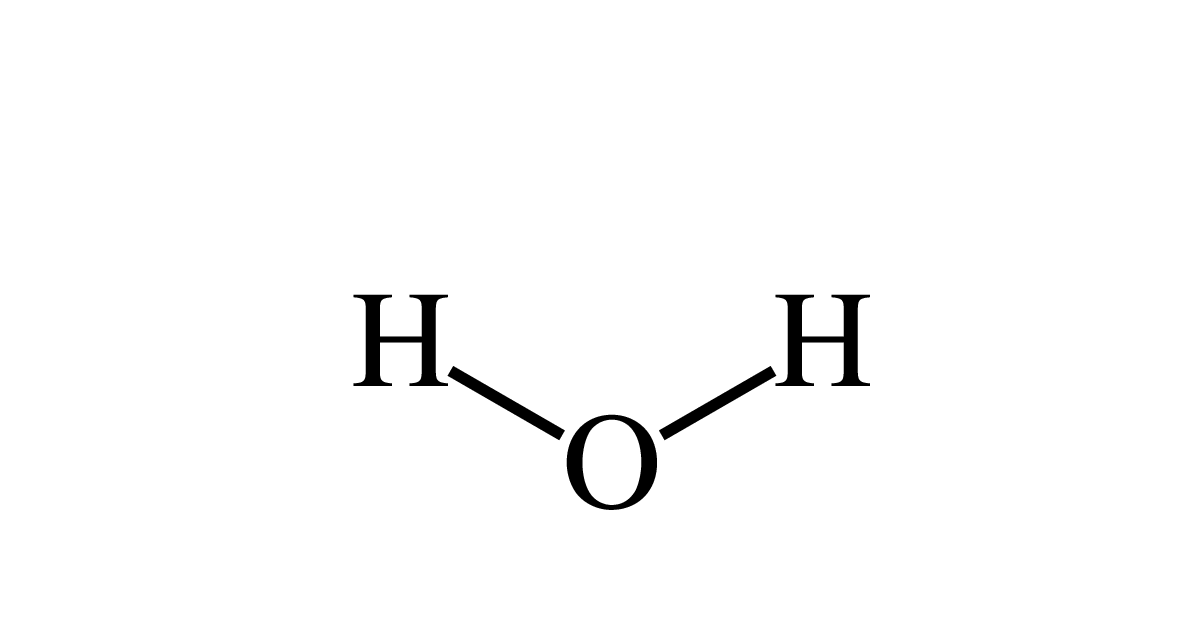
(a) Water
| atoms | ||
|---|---|---|
| 2.5369 | -0.1550 | O |
| 3.0739 | 0.1550 | H |
| 2.000 | 0.1550 | H |
| bonds | ||
|---|---|---|
| 1 | 2 | 1 |
| 1 | 3 | 1 |

(b) Ethylene
| atoms | ||
|---|---|---|
| 2.0000 | 0.0000 | C |
| 3.0000 | 0.0000 | C |
| 1.6900 | 0.5369 | H |
| 1.6900 | -0.5369 | H |
| 3.3100 | -0.5369 | H |
| 3.3100 | 0.5369 | H |
| bonds | ||
|---|---|---|
| 1 | 2 | 2 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 2 | 5 | 1 |
| 2 | 6 | 1 |
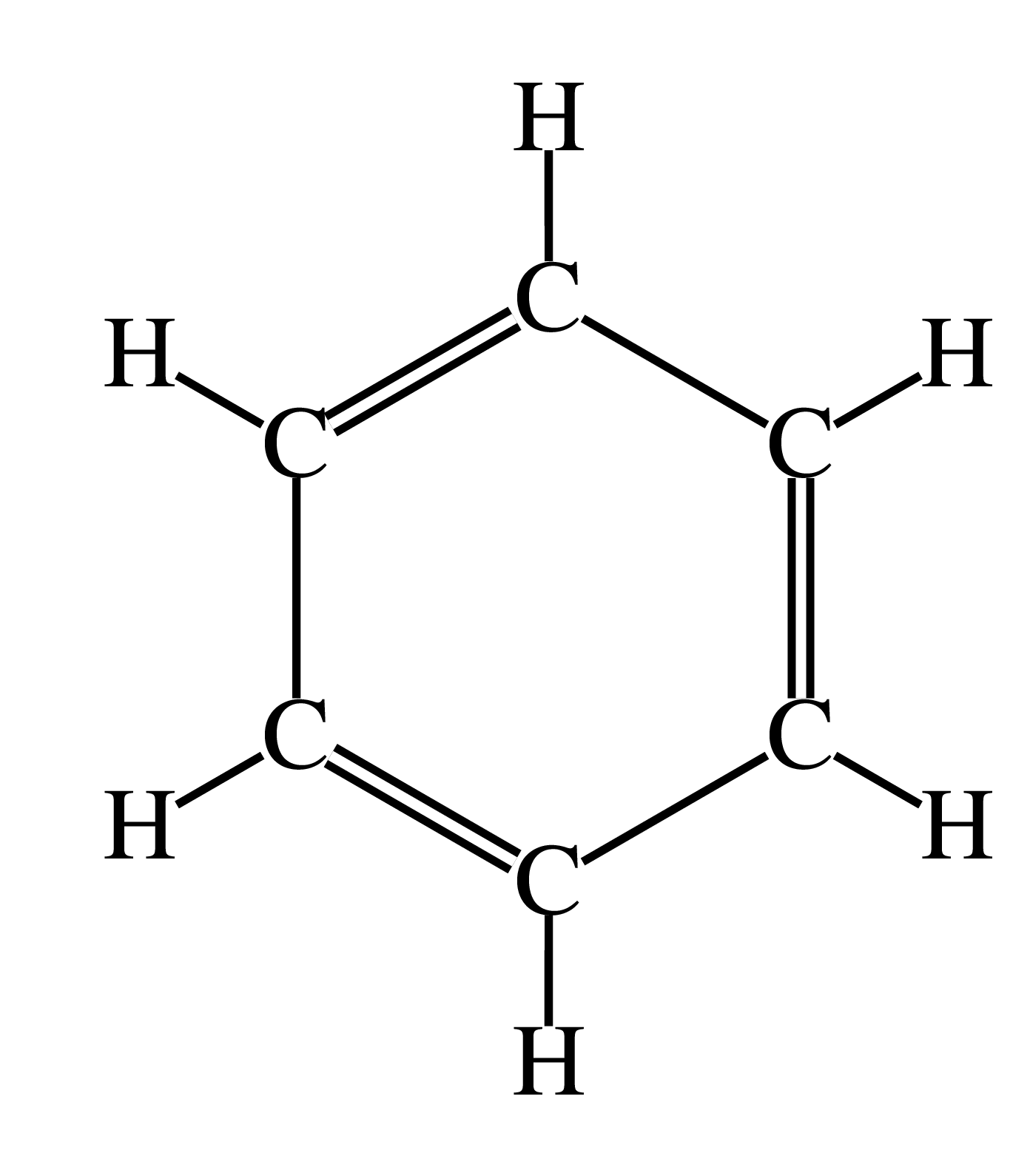
(c) Benzene
| atoms | ||
|---|---|---|
| 2.8660 | 1.0000 | C |
| 2.0000 | 0.5000 | C |
| 3.7320 | 0.5000 | C |
| 2.0000 | -0.5000 | C |
| 3.7320 | -0.5000 | C |
| 2.8660 | -1.0000 | C |
| 2.8660 | 1.6200 | H |
| 1.4631 | 0.8100 | H |
| 4.2690 | 0.8100 | H |
| 1.4631 | -0.8100 | H |
| 4.2690 | -0.8100 | H |
| 2.8660 | -1.6200 | H |
| bonds | ||
|---|---|---|
| 1 | 2 | 2 |
| 1 | 3 | 1 |
| 1 | 7 | 1 |
| 2 | 4 | 1 |
| 2 | 8 | 1 |
| 3 | 5 | 2 |
| 3 | 9 | 1 |
| 4 | 6 | 2 |
| 4 | 10 | 1 |
| 5 | 6 | 1 |
| 5 | 11 | 1 |
| 6 | 12 | 1 |
What properly constitutes a data model?
If, rather than by blindly following current practice, we are to understand what should properly constitute a data model from first principles then we need decide whether the principle of the identity of indiscernibles should be included among these. The argument for the principle runs alongs the lines that a data model is a theory of various sorts of things that are in some sense real to us and which for convenience we call ‘real world entities’; databases hold data according to this model and represent these real world entities and relationships. Clearly, goes the argument, there must be an unambiguous correspondence between the real word entities and their representations within the database instance — of necessity from the properties of a database entity, a unique real word entity with matching properties must correspond. For this to be achieved then it must be so that no two distinct database entities nor any two real world entities may have exactly the same properties, which is to say that the principle of identity of indiscernibles must hold true both of entities within database instances but also of real world entities. The counter argument is basically the Max Black counter argument given earlier and as illustrated by the molecular structure example — the real world that we wish to represent just might have indiscernibles that are identical. The answer to this dilemma in relational data modelling is to (i) enforce the indiscernibility of identicals in the database model (ii) accept that the principle may not hold of real world entities and thus (iii) to require the introduction of arbitrary distinguishing properties that have no basis in the real world but are simply artefacts introduced for descriptive purposes. In the case of descriptions of molecular structure it is common practice, as instanced in the Pubchem database, that the ‘arbitrary distinguishing property’ takes the form of an ordinal — one is assigned to each atom within the structure, in nature there is no such ordinal nor any other such distinguishing feature.
First Principles of Data
In early computer systems data was said to be stored in records within files and this terminology kept contact with the paper systems whose use preceeded computerisation. Subsequently, driven by E.F. Codd, there was a shift of predominant terminology to data being said to be held in rows within tables, equally, in the accompanying theory, rows are described, unhelpfully it seems to me, as tuples. At the risk of confusing matters further, but with foundations at heart, I will use instead the term message in place of either record or row or tuple.
In building Information Systems the fundamental principles of data need include those regarding the identification of subject entities as described above and to which we can add these:
- there are subject entitites and they are of a fixed number of types,
- data consists of messages, each message describes a subject entity,
- messages have a structure and messages describing the same type of subject entity have the same structure.
If a database is a set of messages able to communicate entitites then what, from first principles, is the message structure? The most general statement that we can make is that a message comprises a set of attributes of the subject entity and that the message structure is agreement upon the set of attributes and the message representation corresponding to each type of subject entity.
Earlier we said that asking What is data? is a bit like asking What is language?. So, in looking for the first principles of data modelling we might look for help at linguistics. In a book written by Jonathan Culler summarising the work of the man sometimes said to be the father of linguistics, Ferdinand de Sassure, we find Alfred North Whitehead quoted:
For the data shown in figure 7 we can describe individual rows in message structures like this:
In these descriptions atom and bond are types of entity and therefore types of message and atomNo, x, y, elementSymbol, atom1No, atom2No and bondtype are attributes. Of these attributes atomNo and bondNo are referential attributes which identify the subject entity of their respective messages and atom1No and atom2No are referential identifying the atoms which bonds link i.e. to which they are related.Entity Models as Data Models
When entity models are used to specify data models they define the types of subject entities and for each such type the attributes used to communicate entitites of that type. They also define which attributes are referential and the relationships they represent inclusive of which referential attributes identify the subject entity of each message.