Questions of commutativity are very important in how data is represented - in saying this we need to clarify that by commutativity we make reference to the commutative diagrams that form the basis of category theory whether expresed in diagrams or in equations or in some other form and that by the term data representation we mean to include both the tabular relational means of storing and presenting data and also such hierarchical data representations as are familiar in, but not restricted to, XML documents. What is described here is essentially about the means of anaphorical reference, whether we talk strictly of data or of communication generally; its relevance goes beyond a strict computer science interpretation.

In the terminology of Ellis Ellis, HC. A Refined Model for Definition of System Requirements. Database Journal, 12(3):2--9, 1982. , wherever in an entity model there is a path of single-valued relationships:

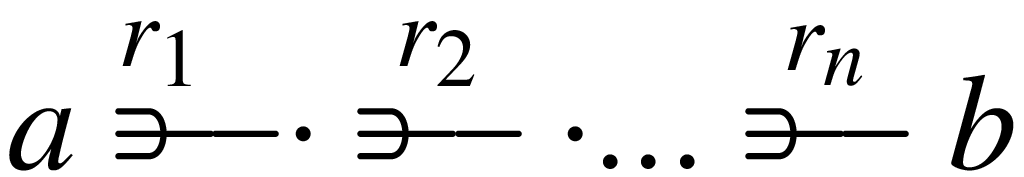
then the destination entity type b is said to be in the logical horizon of the source entity type a. In programming, equivalently, we might say that it was possible to navigate from any one a to a definitive other b. Now if there are two such navigation paths between entity type a (the source) and entity type b (the destination) then a question naturally arises as to whether following one path is equivalent to following the other i.e whether starting at any entity of type a we arrive at the same destination entity of type b regardless of which of the two paths we follow. In an abstract mathematical setting, diagrams showing such equivalent paths are said to be commutative diagrams and methods of reasoning using such diagrams is the starting point of category theory.

Scope diagrams of mandatory relationships are examples of near commuting diagrams, techically they only commute if the relationships whose scope they describe is specifed to be mandatory i.e cardinality One rather than Zero Or One. For instance there are examples of such commuting scope diagrams here: The Scope Concept.

The questions that are important for how data is represented concern the commutativity of diagrams of relationships - which diagrams commute - which is to say if one were to navigate the entitites and relationships to be represented in the data which navigational paths are equivalent? Understanding and agreeing the answer is cruical to data representation and interpretation, as we now illustrate.

Now we can adjust an earlier example to get to the nub of the matter. If the paths f/g and h are equivalent then attribute fgname in both relational and hierarchical models has always the same value as the attribute fname. It is therefore redundant and should be omitted from the data model.

Figure 1

Three equivalent models: logical model at the top, relational model in the middle, an hierarchical model at the bottom.

Another example is shown in figure 2.